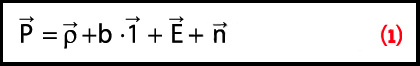Q: Why is acquisition of GNSS signals generally more difficult than tracking and what are the limiting factors?
A: A fairly good analogy of the difference between GNSS signal acquisition and tracking can be found in the rescue of victims of a sunken ship whose location is not accurately known. The first stage of the rescue attempt typically involves an aircraft flying a search pattern, which hopefully encompasses the location where the ship went down.
For two main reasons, spotters aboard the plane may have great difficulty finding a person afloat in a vast expanse of ocean. First, because the human eye is most sensitive in its relatively small area of central vision, the spotter must scan over a wide area to locate what appears to be a tiny spot on the ocean’s surface. Second, detecting a human figure can be very difficult among numerous whitecaps whipped up by the wind in a rough sea, which appears as “noise.”
The process of searching for a person at sea is analogous to the search required for acquisition of a GNSS signal.
However, once the victim is located (acquired), the spotters must keep the person in sight (tracked) for some period of time during rescue operations. The tracking process is generally much easier than acquisition, as the spotter now knows quite accurately where the person is located.
In this phase, the sophisticated tracking capability of the eye’s central vision area comes into play. Even momentary disappearance of the victim is not a problem, because reliable reacquisition is possible by performing a search over a very small area, and the clutter (noise) outside this area can be disregarded. This type of operation is analogous to tracking a GNSS signal.
For concreteness, we will compare the acquisition and tracking processes for a legacy L1 C/A-coded GPS signal from a single satellite, with simplifications that facilitate understanding. In this case acquisition sensitivity is defined as the minimum signal power required for a specified reliability of correct acquisition, with a similar definition for tracking sensitivity.
Although with enough processing there is no theoretical limit for either, the sensitivity for tracking in GPS receivers is generally better (typically about two to five decibels lower in signal power) than for acquisition.
Why does this happen?
When a typical GPS receiver is turned on, the following sequence of operations must occur before the receiver can access the information in a GPS signal and use it to provide a navigation solution:
1. Determine which satellites are visible to the antenna.
2. Determine the approximate Doppler of each visible satellite.
3. Search for the signal in both C/A-code delay and frequency (i.e., Doppler shift).
4. Detect a signal and determine its code delay and carrier frequency.
5. Track the C/A-code delay and carrier frequency as they change.
Signal Acquisition
The acquisition process consists of Steps 1–4 in the foregoing list. In Steps 1 and 2 the visible satellites and approximate Doppler shifts are usually found using approximate time, approximate receiver position, and almanac data (for satellite position and velocity) — all of which have been previously stored in the receiver. This permits the receiver to establish a frequency search region for each visible satellite, and is similar to establishing the region of ocean to search in the above analogy.
Step 3 requires by far the most computation. The C/A-code search is necessary because GPS signals are spread-spectrum signals in which the C/A code spreads the total signal power over a wide bandwidth, dropping its power density well below that of a receiver’s thermal noise. A signal is therefore virtually undetectable unless it is de-spread to a much narrower bandwidth by correlation with a replica code in the receiver that is precisely time-aligned with the received code.
Because the signal cannot be detected until alignment has been achieved, a search over all possible alignment positions is required. For each trial code alignment position, the signal must be averaged over a sufficiently long time period to build up the signal-to-noise ratio (SNR) to a usable level.
Such averaging requires that the receiver be accurately tuned to the received carrier frequency; otherwise the averaging can be severely degraded. However, at L-band the frequency uncertainty of a typical receiver’s reference oscillators and the Doppler uncertainty due to uncertainty in receiver location and velocity can make the tuning uncertainty as large as several kilohertz (satellite motion alone account for approximately ±5 kilohertz at L1). Thus, in addition to the code search, a receiver also needs to search in frequency.
. . .
Signal Tracking
Once the cell containing the signal has been detected in Step 4, typical receivers use code and carrier tracking loops in Step 5 to generate error signals that keep the replica and received codes aligned and also keep the receiver tuned to the correct frequency as changes in Doppler occur. However, a discrete approximation to these methods of tracking is to repeatedly compare the values of S in the current signal cell with the values in the eight cells surrounding it.
Although the approximation is somewhat crude, it makes analysis of tracking sensitivity much easier and does not really falsify our understanding. If the maximum value of S in the surrounding cells exceeds that of the central cell, the cell with that maximum value is declared as the new signal cell. In this way, both the code delay and carrier frequency of the received signal can be tracked by repeatedly performing a local search over only N = 9 cells, each local search resulting in a tracking update.
. . .
To summarize, with enough processing, no theoretical limit exists for either acquisition or tracking sensitivity. However, because tracking requires examination of only a local code delay and carrier frequency region (and coherent averaging can be used as well over the full length of data bits in legacy L1 GPS signals), tracking can be made more sensitive than acquisition before cost limits (either in hardware or processing time) are reached.
Similar conclusions can be reached for other GNSS signals, even taking into account differences in their characteristics.
(For Lawrence Weill’s complete answer to this question, including formulas and tables, please download the full article using the pdf link above.)