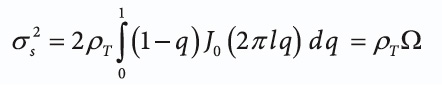Equation: signal variance for a “ring of scatterers” modelIndoor GNSS propagation environments are characterized by multiple reflected signal paths (multipath) terminating at the receiver. Consequently, the received signal’s amplitude, phase, and perceived angle of arrival attributes vary randomly as the receiver moves. This has created significant interest among receiver designers and manufacturers to develop powerful processing for GNSS handsets such that these can operate effectively in indoor faded environments.
Indoor GNSS propagation environments are characterized by multiple reflected signal paths (multipath) terminating at the receiver. Consequently, the received signal’s amplitude, phase, and perceived angle of arrival attributes vary randomly as the receiver moves. This has created significant interest among receiver designers and manufacturers to develop powerful processing for GNSS handsets such that these can operate effectively in indoor faded environments.
Typically, to overcome the low signal strength generally associated with indoor environments, receiver signal-processing designs use longer coherent integration times. However, the processing gain that is achievable by merely relying on coherent integration of arbitrarily long duration is limited. The channel decorrelates both spatially and temporally, which directly imposes a limit on the effective coherent integration interval of the handheld receiver when the antenna is undergoing some form of translational motion.
Recently, several efforts have been considered to extend the coherent integration time by aiding the process with auxiliary sensors. Using a Rayleigh fading model, our research shows that, for a moving antenna in a typical indoor multipath environment, the processing gain saturates as the coherent interval increases. Consequently, beyond a certain integration interval, no further processing gain can be extracted directly from coherent integration.
In this article, we seek to derive and quantify the limits of coherent integration due to spatial decorrelation using experimental verification. Our ultimate goal is to determine the coherent integration gain limit for various fading scenarios and antenna motion. This information, in turn, could be used to select optimal coherent integration times in commercial grade chipset receivers in order to help set appropriate Doppler search bin steps and, by these efforts, reduce the receiver processing load.
System Model
In the diffuse Rayleigh-faded multipath environments explored in our investigation, the channel gain can be modeled by a complex normal (CN) random variable, as described in the article by B. Friedlander et alia cited in the Additional Resources section. The channel gain is a random process with a coherence time that depends on how fast the channel decorrelates spatially and temporally.
To extract the GNSS signal buried in noise, the receiver accumulates a temporal snapshot of the received signal over the snapshot interval T. Assume that during the snapshot interval, the antenna moves with a constant velocity v. As discussed in the article by A. Broumandan et alia listed in Additional Resources, after some manipulation and normalization the signal variance for a “ring of scatterers” model can be shown to be
(See equation, above right.)
where ρT is the average signal-to-noise ratio (SNR) as signal energy in a T second interval, Ω is defined as the moving antenna correlation coefficient, and J0 is the zero-order Bessel function of the first kind.
The problem of interest here is comparing the coherent integration time limit of a receiver in motion to one that is static. If the signal SNR in the moving case is defined as a function of the velocity v and the snapshot interval T as ρTΩ(v,T), the normalized integration gain (NIG) metric — which is the ratio of the integration gain of a moving antenna to the integration gain of the static antenna for T=1 — can be defined as NIG = Ω(v,T)ρT /ρT=1.
The NIG metric in fading environments depends on several factors, including antenna trajectory and velocity as well as the geometry of the scatterers. To evaluate the performance of coherent integration in a multipath environment, a linear motion with constant velocity is considered. We also assumed that the antenna trajectory and incoming signals are located in the same plane and that signals are coming from a sector with an angular spread of φs.
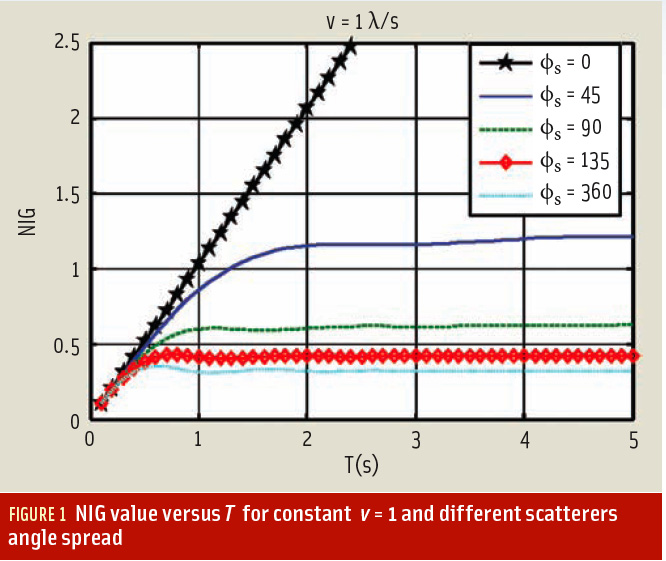
Figure 1 shows the NIG value for v = 1 λ/s and for angular spreads of 0, 45, 90, 135, and 360 degrees. In the range of T ∈ {0, 0.5} the integration gain is almost linearly increasing by T for all cases. Hence, increasing integration time enhances the processing gain.
However, due to receiver motion and signal decorrelation, increasing T further cause decorrelation of signal samples for the case of φs = 360 and φs = 135. Thus, after approximately one second the processing gain of the coherent integration remains constant and becomes independent of T. Note that in the case of φs = 0 the NIG value given in Figure 1 linearly increases with the slope of one implying that increasing integration time will increase the processing gain.
As shown for the cases of φs > 90, the processing gain is saturated after a carrier wavelength receiver displacement. Hence, even knowing the exact trajectory will not improve the processing gain.
Experimental Results
Experimental measurements are based on the indoor reception of GPS L1 C/A signals. A dual-channel front-end was used to down-convert GPS raw data to the baseband frequency.
To account for the navigation data modulation, reference signals were collected from a static antenna located on the rooftop within 10 meters above the measurement area under line-of-sight conditions. These reference signals were sampled in a synchronous fashion with the signals received indoors. Live GPS signals were collected in a large room located in the commercial office building. After down-conversion GPS signals were sampled by a digitizer unit, and raw digital complex samples were stored in a computer.
In the room, an active antenna mounted on a linear moving table was used to create a moving-receiver scenario with a constant velocity. During the data-collection process the antenna was moved back and forth with a constant speed of 0.5 meter/second on a two-meter linear trajectory.
Before evaluating the coherent integration performance in the moving mode, we conducted a static antenna test. Experimental results of coherent integration performance in this indoor static case showed that no integration loss occurred due to the temporal decorrelation during the coherent integration time of 1.6 seconds.
During the despreading processes a frequency search by the maximum Doppler frequency centered at the reference antenna frequency was adopted with the peak of the correlation function selected as the test statistic. We considered various coherent integration times (CITs) to evaluate the integration performance. The mean values for each CIT are tabulated in Table 1.
Figure 2 shows the measured SNR of the various CITs values for an observation time of four seconds for the moving and static antenna process. Considering the results of Table 1, processing gain continues to increase even when the coherent integration time is extended to 1,600 milliseconds, which is equivalent to an antenna displacement of four wavelengths.
To justify this contradiction, consider the first 1.6 seconds of SNR values shown in Figure 2a. If one takes the maximum values of each CIT case during this observation time (1.6 seconds), we can see that they all have almost the same maximum SNR values — about 18 decibels. This phenomenon cannot be detected in the SNR variation of the static antenna case shown in Figure 2b.
On the other hand, if the observation time is 1.6 seconds, it does not matter if we coherently integrate for 1.6 seconds or use four successive 400-millisecond integration subsets and take the subset with the maximum signal power. This latter scheme selects the maximum value of a portion of data set in each observation time that has the maximum energy for a given correlated subset of data.
This is similar to the selection diversity system described in the book by J. D. Parsons listed in Additional Resources. In the “ideal” selection diversity system, Parsons states, “the signal with the highest instantaneous [carrier to noise ratio] CNR is used, so the output CNR is equal to that of the best incoming signal.”
To verify the selection diversity process further, the probability density function (PDF) of the measured SNRs for different integration times are shown in Figure 3a. In Figure 3b, Max (τ, k) expresses the PDF of a scenario for which the observation time is T=τk milliseconds. The maximum SNR values at the output of k successive τ ms coherent integration is considered to yield the Max (τ, k) plot.
As shown in Figure 3b, for a given observation time, different integration scenarios carry almost identical SNR PDFs, which further confirms that the processing gain shown in Table 1 is due to the selection diversity process and not to coherent integration gain.
Conclusions
This article has considered the coherent integration performance of GNSS signals for a moving antenna in a diffuse fading environment. Our ultimate goal was to determine the coherent integration gain limit for various fading scenarios and antenna motion.
From the theoretical perspective, we have shown that the coherent integration gain of a moving antenna is limited due to spatial decorrelation such that the CIT should be commensurate with an antenna displacement. Our analysis has also shown that in a case where the angular extent of the multipath scattering is wide, knowledge of the antenna trajectory is of no benefit to enhancing the processing gain. Experimental measurements were performed to verify the assumption of the Rayleigh fading and the diffuse scattering model.
However, the experimental results seemingly contradicted the theoretical asymptotic limit of the processing gain that is available by increasing integration time. By increasing processing time, SNR values surpassed the theoretical asymptotic limit due to selection diversity. The coherent integration time limit in fading environments leads to saturated processing gain, but by adding incremental processing based on the selection diversity process, the processing gain can be extended.
The coherent integration time limits investigated in this article could be taken into account to choose optimal coherent integration times in commercial grade chipset receivers operating in the indoors and in high multipath environments. This, in turn, would enable handset designers to set appropriate Doppler search bin steps and consequently reduce the receiver processing load.
Additional Resources
[1] Broumandan, A., and J. Nielsen and G. Lachapelle
“Enhanced Detection Performance of Indoor GNSS Signals Based on Synthetic Aperture,” IEEE Transactions on Vehicular Technology, Vol. 59, NO.6, July 2010
[2] Friedlander, B., and S. Scherzer, “Beamforming Versus Transmit Diversity in the Downlink of a Cellular Communications Systems,” IEEE Transactions on Vehicular Technology, vol. 53, no. 4, July 2004
[3] Parsons, J. D., The Mobile Radio Propagation Channel, John Wiley & Sons Ltd., Second edition, 2000
